Funktionen-theorie
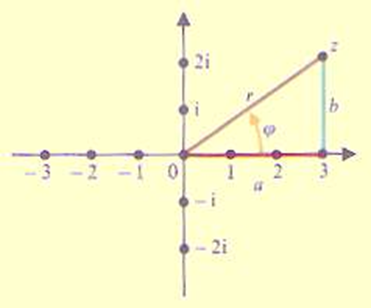
Gaußsche Ebene der komplexen Zahlen
z=a+bi
r²=a²+b²=|z|²
In der Funktionentheorie beschäftigt man sich mit Funktionen einer komplexen Veränderlichen mit Werten im Körper C der komplexen Zahlen. Zum Beispiel lassen sich Funktionen wie cos, sin und die Exponentialfunktion vom Reellen ins Komplexe fortsetzen, (die Exponentialfunktion wird dann allerdings periodisch). Es gibt den Begriff der komplexen Differenzierbarkeit. Komplex differenzierbare Funktionen haben die nützliche Eigenschaft, dass ihre Ableitung stets wieder komplex differenzierbar ist. So kommt man in einer Vorlesung über Funktionentheorie auch schnell zu schönen Anwendungen wie zum Beispiel zu einem Beweis des Fundamentalsatzes der Algebra, der besagt, dass jedes nicht konstante Polynom mit komplexen Koeffizienten eine Nullstelle in C hat.
Der sogenannte (komplexe) Residuensatz findet Anwendung in der Berechnung uneigentlicher reeller Integrale. Daher ist die Funktionentheorie auch für Studierende der Physik interessant.
Die Vorlesung Funktionentheorie kann man ab dem dritten Semester eines Mathematik- oder auch Physikstudiums hören. Mögliche weiterführende Vorlesungen behandeln z.B. Funktionentheorie mehrerer komplexer Veränderlicher, Riemannsche Flächen, analytische Zahlentheorie, Funktionalanalysis, komplex projektive Varietäten und Liegruppen.