Differential-gleichungen
Bei den Differentialgleichungen zeigt sich die Anwendbarkeit der Mathematik in Naturwissenschaft und Technik besonders deutlich. So gilt zum Beispiel bei geradliniger Bewegung für die Geschwindigkeit v(t) und die zurückgelegte Weglänge s(t) die Gleichung s'(t)=v(t), wobei s‘ die Ableitung nach der Zeitvariablen t bezeichnet. Die Funktion s nennt man eine Lösung der Differentialgleichung s’=v(t).
Allgemein nennt man eine Gleichung der Form y(n) = f(x, y, y‘,…, y(n-1)) eine gewöhnliche Differentialgleichung n-ter Ordnung. Hierbei sei f eine reellwertige stetige Funktion auf einer Teilmenge G von Rn+1. Eine Lösung ist eine n mal auf einem reellen Intervall I differenzierbare Funktion y, die für jedes x aus I die beiden folgenden Bedingungen erfüllt: Der Punkt (x, y(x), y'(x) ,…, y(n-1)(x)) liegt in G, und es ist y(n)(x) = f(x, y(x), y'(x) ,…, y(n-1)(x)).
Wir betrachten einige Beispiele, wobei wir die Abkürzung DGL für „Differentialgleichung“ benutzen:
- Die Gleichung y’=y ist eine DGL 1.Ordnung. Man sieht sofort, dass y(x) = ex eine Lösung ist. Tatsächlich ist yc(x) = c ex für jede Konstante c aus R eine Lösung, und es ist I=R.
- Die Gleichung y“ = – y ist eine DGL 2.Ordnung. Eine partikuläre Lösung ist y(x)=cos(x), denn es ist y'(x)=-sin(x) und also y“(x)=-sin’x=-cos(x)=-y(x). Eine allgemeine Lösung ist die Funktion y(x) = c1cos(x) + c2sin(x).
- Die Gleichung y’= -x-1 y ist eine DGL 1.Ordnung mit allgemeiner Lösung y(x) = c x-1, es ist y'(x) = -c x-2 = – x-1 y(x). Durch Vorgabe einer Anfangswertbedingung kann man die Lösung eindeutig machen, zum Beispiel soll y(1)=27 gelten. Dann hat man nur eine Lösung, nämlich y(x) = 27 x-1.
- Die Gleichung y’= a(x) y mit einer stetigen Funktion a hat Lösungen der Form y(x) = c eA(x), wobei A irgendeine Stammfunktion von a ist und also A‘ = a erfüllt. Man nennt diese Gleichung eine homogene lineare DGL 1.Ordnung.
- Lösungen der inhomogenen linearen DGL y’=a(x)y+b(x), wobei b(x) stetig und nicht Null ist, erhält man nach einer Idee von Lagrange (1736-1813) durch Variation der Konstanten. Man macht einen Ansatz y(x)=c(x)eA(x), wobei A eine Stammfunktion von a ist, und erhält y'(x)=a(x)y(x)+c'(x)eA(x). Vergleich mit der vorgegebenen DGL ergibt dann die unten in IV angegebenen Lösungen.
Man beachte, dass eine Stammfunktion stets nur bis auf eine additive Konstante C bestimmt ist. In der folgenden Tabelle sind einige einfachere DGL-Typen 1.Ordnung mit möglichen Lösungsmethoden aufgelistet.
| Typ | Lösungen y(x) | |
| I | y‘ = f(x) | |
| II | y‘ = g(y) | Löse folgende Gleichung nach y auf: |
| III | Getrennte Variable y‘ = f(x)g(y) | Löse folgende Gleichung nach y auf: |
| IV | Inhomogene lineare DGL y’= a(x)y+b(x) und b nicht 0 | Variation der Konstanten eA(x) ( |
| V | Bernoulli-DGL y‘ = f(x)y + h(x)yr, r aus R | Substitution z=y1-r ergibt z’=(1-r)f(x)z+(1-r)h(x), also Typ IV |
| VI | Ricatti-DGL y‘ = f(x) + g(x)y + h(x)y² | Falls partikuläre Lösung u gefunden: Sustitution z=y-u ergibt z’=(g(x)+2h(x)u(x))z+h(x)z², also Typ V |
| VII | y‘ = f(x-1y) | Substitution z=x-1y ergibt z’=x-1(f(z)-z), also Typ III |
| VIII | Spezielle Riccatti-DGL y‘ = ax-2 + by2 mit a,b aus R | Substitution z=y-1 ergibt z’=-b-a(x-1z)2, also Typ VII |
Man muss hierbei sehr aufpassen, zum Beispiel muss natürlich g(y) ungleich 0 in II und III gelten. In einer Vorlesung über gewöhnliche Differentialgleichungen werden Kriterien über die Existenz von Lösungen und deren Eindeutigkeit bei vorgegebener Anfangswertbedingung hergeleitet.
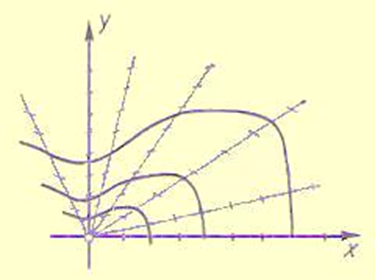
In der allgemeinen Lösung einer gewöhnlichen DGL der Ordnung n hat man n freie Konstanten. Ist n=1, so ist durch die DGL y’=f(x,y) in jedem Punkt P einer jeden Lösungskurve yc(x) eine Steigung vorgegeben (nämlich die Steigung der Tangente an die Kurve im Punkt P). Man spricht dann von einem Richtungsfeld, und in einfachen Fällen kann man an dem Richtungsfeld die Lösung ablesen. Oben auf dieser Seite ist das Richtungsfeld einer DGL vom Typ y’=f(x-1y) aufgemalt.
Ab n=2 kann man statt Anfangswertbedingungen auch Randwertbedingungen stellen, um die Konstanten zu bestimmen. Ist y“=f(x,y,y‘) eine DGL 2.Ordnung, so ist zum Beispiel durch y(x0)=y0 und y'(x0)=y1 eine Anfangswertbedingung und durch y(x0)=y0 und y(x1)=y1 eine Randwertbedingung gegeben. Man unterscheidet hier zwischen Anfangswertaufgaben und Randwertaufgaben.
Untersucht werden auch Systeme von Differentialgleichungen, zum Beispiel kann man ein homogenes lineares System 1.Ordnung mit Hilfe des Matrizenkalküls schreiben als y‘=A(x)y, wobei A(x) eine Matrix ist, und mit Methoden der linearen Algebra behandeln. Hierbei geht dann auch die Theorie der Eigenwerte und Eigenvektoren ein.
Gewöhnliche Differentialgleichungen werden bereits in den Vorlesungen Analysis II oder III betrachtet. Danach kann man dann noch Vorlesungen über gewöhnliche und partielle Differentialgleichungen anschließen. Bei partiellen Differentialgleichungen hängen die Lösungsfunktionen von mehr als einer Variablen ab. Man kann sie bei zwei Variablen x,y zum Beispiel schreiben als f(x,y,z(x,y),zx,zy,zxx,zxy,zyy,…)=0, wobei die Indizes partielle Ableitungen bedeuten.